A ce niveau de 1ère série, nous sommes résolument dans la haute compétition. Le jeu de la carte reste essentiel pour progresser encore, y compris en attaque. Les plans de jeux les plus compliqués, les fins de coup particuliers, tels que les squeezes, seront ici abordés. Comme pour l’ « année » précédente, je me suis largement inspiré, pour les cours et les différents exposés et exemples, de la progression proposée par Robert Berthe (1931-), l’auteur de la célèbre rubrique Pas à Pas de la revue Le bridgeur, et son complice Norbert Lébely, qui, récemment, ont proposé un nouvel ouvrage de perfectionnement. Ici, vous trouverez les cours dispensés par l’auteur de ce site.
Notions probabilités.
Manoeuvre de Buffalo : Moins efficace que l’impasse, mais dernière chance.
Coup sans nom : Coup sans nom 1°) dans l’espace, 2°) dans le temps.
Coup du ciseau : Très similaire au Coup sans nom…
Coup du dentiste : Une élimination pour rentrer en main en sûreté.
Réduction d’atouts : Notions, exemple pour une impasse.
Le squeeze simple (1) : Introduction au squeeze par un exemple.
Le squeeze simple (2) : Le vocabulaire du squeeze.
Réduction du compte : Presque toujours indispensable. La lutte des flancs.
Le squeeze à retardement : Lorsque la réduction du compte est impossible.
Le squeeze fantôme : Le double squeeze va-et-vient droit de Bertrand Romanet.
Faux squeeze : 2 donnes laissant croire à un squeeze…
Ruse du déclarant (1) : Faire croire à une impasse, dissimuler une haute carte.
Ruse du déclarant (2) : Tromper sur la répartition, tromper en défaussant.
Tous ces cours peuvent être retrouvés dans l’Index-Dictionnaire.
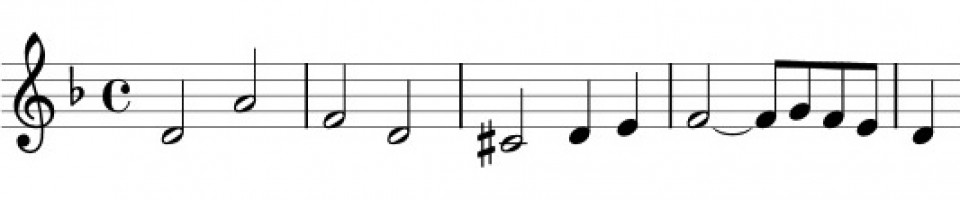

Bonjour,
Je viens de lire l’article ‘Notions de Probabilité’, et je pense que l’exemple ‘3 boites dont l’une contient l’as de Coeur’ prête à confusion. On y reconnait le problème de Monty-Hall … mais sur un plan pédagogique, je pense qu’en l’état, cet exemple est contre-productif.
En dehors de cela, sur le plan purement bridgesque, 100 fois BRAVO !
Cher Monsieur Chailley,
Dans la page « Le squeeze à retardement », sur le premier exemple, vous avez écrit : « Est ne peut pas se dégarder à ♣ ni à ♥ », mais les couleurs sont en fait ♣ et ♦.
Cordialement,
Jean Bréfort
Oui, merci ! C’est corrigé.
Cordialement,
Olivier CHAILLEY